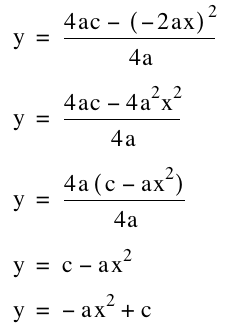Locus of Vertices
by
Susan Sexton
Consider the set of parabolas
graphed from the equation:
![]()
Suppose b ranges from -3 to
3, take a look at the following graphs:
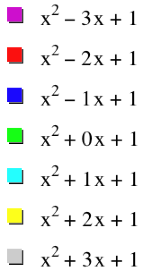
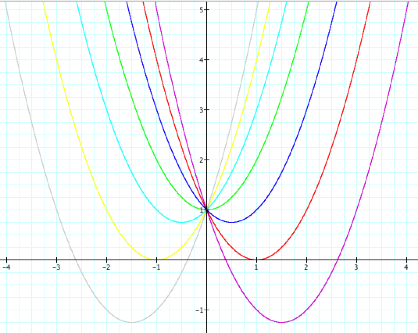
What would be the locus of points of the vertices of the parabolas? Considering the figure below, it appears that it may be a parabola.
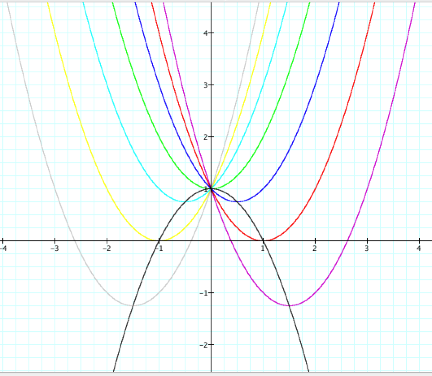
How might this be proved with
the equations given? Consider the
vertices that lie on the graphs of the 7 equations: (0,1), (-1.5, -1.25), (-1,0), (-.5, .75), (.5, .75), (1,0),
and (1.5, 1.25). Lets try to find
the equation of the parabola that goes through these points. It would be easy to focus on vertices
(0,1), (-1,0), and (1,0). I will
solve a system of equations in three variables using:
![]()
By substituting (0,1) we can
see that c = 1 so now we can solve a system of equations in two variables.
Substituting (-1,0) we have:
![]()
Substituting (1,0) we have:
![]()
This means that b = 0 and a =
- 1
So our locus of points is
indeed a parabola whose equation is:
![]()
LetÕs try it again for
another set of parabolas:
![]()
Again, I will let b range from -3 to 3.
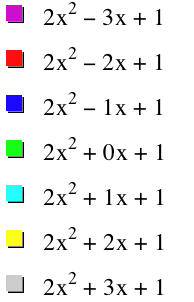
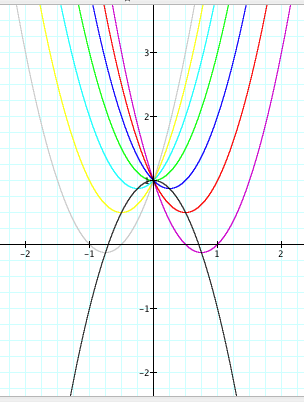
Using the three vertices, (0,
1), (-.5,.5), and (.5,.5) and the same method of algebra as earlier, it can be
verified that the locus of points is the equation:
![]()
Here ÒaÓ is opposite the ÒaÓ
of the original equation and ÒcÓ stayed the same. This occurred earlier too, is this a coincidence? LetÕs try it again and change the value
of ÒaÓ to a fraction and change the value of ÒcÓ to be something different than
the two earlier examples.
Consider:
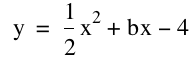
Again, b will range from -3 to 3.
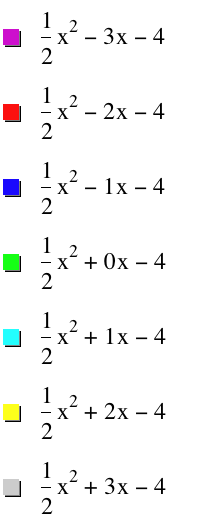
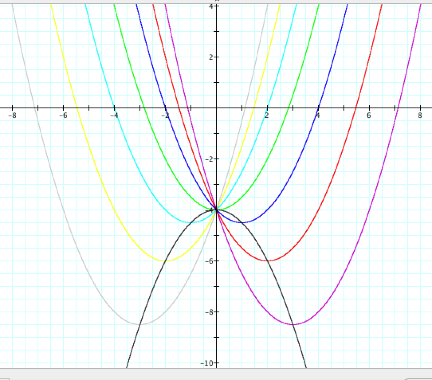
Now I choose the three
vertices, (0, -4), (2, -6), and (-2, -6) it turns out that the locus of
vertices is the equation:
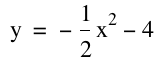
So, indeed it appears that
ÒaÓ will be opposite the original ÒaÓ and Òc" will be the same.
I canÕt resist trying one
more to see if this will work if the parabolas open down. Let ÒaÓ be a negative number.
Consider:
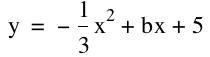
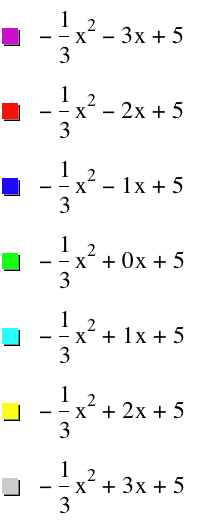
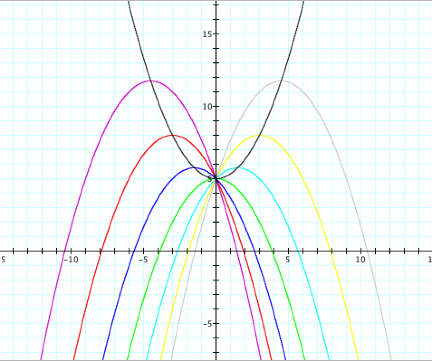
It does appear that the
equation of the locus of vertices has an ÒaÓ value opposite the original. When considering the vertices (0,5),
(-3,8), and (3,8) it can be verified that the locus of vertices is:
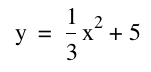
Considering the set of
parabolas:
![]()
(the quadratic equation in standard form)
The locus of vertices is:
![]()
Why does this work?
We know that all parabolas will
have the point (0,c) and its specific vertex on it. What is the vertex in terms of a, b, and c? Another form for the quadratic equation
in standard form is the quadratic equation in vertex form:
![]()
(h,k)
is the vertex
What is (h, k) in terms of a,
b, and c? I will complete the
square to find this out:
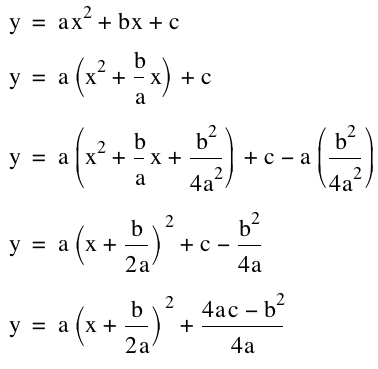
So . . .

Well since ÒhÓ is the ÒxÓ
value of the vertex and ÒkÓ is the ÒyÓ value of the vertex, we can really say:
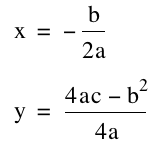
Solving for ÒbÓ we get:
![]()
Substituting ÒbÓ in ÒyÓ we
get: